Heslovitý strukturovaný postup řešení úlohy je instrukcí pro AI, jak přeformulovat postup řešení do vhodné srozumitelnější podoby.
-
Markdown je textový formát, který umožňuje snadnou úpravu.
-
Specifikujte ve vybraném nástroji jaký výsledek očekáváte
- dle obsahu - stručné, do hloubky, začátečník, pokročilý, atd.
- dle formy - video, audio, text, atd.
- dle stylu - formální, neformální, přátelský, odborný, atd.
- dle délky - krátký, střední, dlouhý, atd.
- dle jazyka - český, anglický, atd.
Doporučení pro vytvoření efektivního promptu pro AI. Prompt guide
Náhled
VÝCHOZÍ TEXT K ÚLOZE 1
===
> Třímetrovou dárkovou stuhu jsme dvěma střihy rozdělili na tři díly různých délek.
> Nejprve jsme odstřihli čtvrtinu stuhy na první dárek, potom jsme odstřihli dvě pětiny zbytku stuhy na druhý dárek a poslední díl jsme použili na třetí dárek.
>
> (*CZVV*)
# 1 Vypočtěte, kolik cm stuhy jsme použili na třetí dárek.
---
**1 Rozbor řešení úlohy**
Vyjádři poměrem zbytek z stuha celkem?
- **1. dárek** z **stuha celkem**=1/4
- [COMPLEMENT]
Výpočet: 1 - 1/4 = 3/4
Závěr:**zbytek** z **stuha celkem**=3/4
Vypočti zbytek(m délka)?
- **stuha celkem**=3 __m délka__
- **zbytek** z **stuha celkem**=3/4
Výpočet: 3/4 * 3 = 2,25
Závěr:**zbytek**=2,25 __m délka__
Vyjádři poměrem 3. dárek z zbytek?
- **2. dárek** z **zbytek**=2/5
- [COMPLEMENT]
Výpočet: 1 - 2/5 = 3/5
Závěr:**3. dárek** z **zbytek**=3/5
Vypočti 3. dárek(m délka)?
- **zbytek**=2,25 __m délka__
- **3. dárek** z **zbytek**=3/5
Výpočet: 3/5 * 2,25 = 1,35
Závěr:**3. dárek**=1,35 __m délka__
Převeď 1,35 (m délka) na cm.
- **3. dárek**=1,35 __m délka__
- převod na cm
Výpočet: 1,35 * 100 = 135
Závěr:**3. dárek**=135 __cm délka__
---
# 2
Poměr dvou neznámých přirozených čísel je 4∶5 a dvojnásobky těchto dvou čísel se liší o 6.
**Určete menší z obou neznámých čísel.**
[!NOTE]
Doporučení: Úlohy 3.2, 4.3 a 5 řešte přímo v záznamovém archu.
---
**2 Rozbor řešení úlohy**
Vypočti porovnání větší číslo a menší číslo
- dvojnásobky dvou čísel se liší o 6, tak samotná čísla se musí lišit o 3.
Závěr:**větší číslo** více než **menší číslo** o 3
Vypočti menší číslo?
- **větší číslo** více než **menší číslo** o 3
- **poměr** **menší číslo**:**větší číslo** v poměru 4:5
- **menší číslo**
Výpočet: 3 / |5 - 4| * 4 = 12
Závěr:**menší číslo**=12
---
VÝCHOZÍ TEXT K ÚLOZE 6
===
> Na odvoz beden ze skladu se používají dva různí roboti A, B.\
> Ve skladu bylo 95 beden.\
> Bedny nejprve odvážel robot A, a to po 5 kusech. Jezdil v pravidelných intervalech a odvezl ze skladu za 2 hodiny celkem 50 beden.\
> Pak pokračoval robot B, který vozil bedny jen po 3 kusech, avšak v kratších pravidelných intervalech. Odvezl tak ze skladu za 1,5 hodiny zbývajících 45 beden.
>
> (*CZVV*)
# 6
## 6.1 **Vyjádřete** v základním tvaru **poměr** počtu beden odvezených ze skladu za 1 hodinu robotem A ku počtu beden odvezených za 1 hodinu robotem B.
## 6.2 **Vyjádřete** v základním tvaru **poměr** počtu jízd robota A za hodinu ku počtu jízd robota B za hodinu.
## 6.3 **Vypočtěte**, kolik beden by ze skladu odvezli za 36 minut oba roboti dohromady při společném provozu.
---
**6.1 Rozbor řešení úlohy**
Rozděl 50 (bedna) rovnoměrně 2 krát
- **robot A**=50 __bedna__
- **robot A**=2 __hodina doba__
- [RATE]
Výpočet: 50 / 2 * 1 = 25
Závěr:**robot A** 25 __bedna__ per __hodina doba__
Rozděl 45 (bedna) rovnoměrně 1,5 krát
- **robot B**=45 __bedna__
- **robot B**=1,5 __hodina doba__
- [RATE]
Výpočet: 45 / 1,5 * 1 = 30
Závěr:**robot B** 30 __bedna__ per __hodina doba__
Vyjádři poměrem mezi robot A:robot B?
- **robot A** 25 __bedna__ per __hodina doba__
- **robot B** 30 __bedna__ per __hodina doba__
- [RATIOS]
Výpočet: 25:30 = 5:6
Závěr:**poměr odvezeného množství beden** **robot A**:**robot B** v poměru 5:6
**6.2 Rozbor řešení úlohy**
Vypočti robot A(počet jízd)?
- **robot A** 25 __bedna__ per __hodina doba__
- **robot A** 5 __bedna__ per __počet jízd__
Výpočet: 25 / 5 = 5
Závěr:**robot A**=5 __počet jízd__
Vypočti robot B(počet jízd)?
- **robot B** 30 __bedna__ per __hodina doba__
- **robot A** 3 __bedna__ per __počet jízd__
Výpočet: 30 / 3 = 10
Závěr:**robot B**=10 __počet jízd__
Vyjádři poměrem mezi robot A:robot B?
- **robot A**=5 __počet jízd__
- **robot B**=10 __počet jízd__
- [RATIOS]
Výpočet: 5:10 = 1:2
Závěr:**poměr počtu jízd** **robot A**:**robot B** v poměru 1:2
**6.3 Rozbor řešení úlohy**
Převeď 36 (min doba) na h.
- **robot A**=36 __min doba__
- převod na h
Výpočet: 36 / 60 = 0,6
Závěr:**robot A**=3/5 __h doba__
Vypočti robot A(bedna)?
- **robot A**=3/5 __h doba__
- **robot A** 25 __bedna__ per __hodina doba__
Výpočet: 0,6 * 25 = 15
Závěr:**robot A**=15 __bedna__
Vypočti robot A(bedna)?
- **robot A**=3/5 __h doba__
- **robot B** 30 __bedna__ per __hodina doba__
Výpočet: 0,6 * 30 = 18
Závěr:**robot A**=18 __bedna__
Vypočti dohromady(bedna)?
- **robot A**=15 __bedna__
- **robot A**=18 __bedna__
- [SUM]
Výpočet: 15 + 18 = 33
Závěr:**dohromady**=33 __bedna__
---
VÝCHOZÍ TEXT A TABULKA K ÚLOZE 7
===
> Do vědomostní soutěže se přihlásilo 10 soutěžících a všichni se zúčastnili 1. i 2. kola.\
> V každém kole získali jednotliví soutěžící 8, 9, nebo 10 bodů. Některé údaje jsou v tabulce.
>
> | |8 bodů|9 bodů|10 bodů|Aritmetický průměr|
> |---|:---:|:---:|:---:|:---:|
> |1.kolo||5|||
> |2.kolo||||9,5|
>
> (*CZVV*)
# 7
## 7.1 V 1. kole bylo soutěžících, kteří získali 8 bodů, o jednoho méně než těch, kteří získali 10 bodů.
**Určete průměrný bodový zisk všech soutěžících v 1. kole.**
## 7.2 Určete, kolik soutěžících mohlo ve 2. kole získat 9 bodů.
Najděte všechna řešení.
---
**7.1 Rozbor řešení úlohy**
Vypočti rozdíl mezi soutěž a 9-bodových
- **soutěž**=10 __soutěžící__
- **9-bodových**=5 __soutěžící__
- [DIFF]
Výpočet: 10 - 5 = 5
Závěr:**8-bodových a 10-bodových dohromady**=5 __soutěžící__
Vypočti 8-bodových(soutěžící)?
- **8-bodových a 10-bodových dohromady**=5 __soutěžící__
- **8-bodových** méně než **10-bodových** o 1 __soutěžící__
- [COMP-PART-EQ]
Výpočet: (5 - 1) / 2 = 2
Závěr:**soutěž**=2 __soutěžící__ po 8 __body__
Co lze vyvodit na základě zadaných předpokladů?
- **9-bodových**=5 __soutěžící__
Závěr:**soutěž**=5 __soutěžící__ po 9 __body__
Vypočti 10-bodových(soutěžící)?
- **8-bodových**=2 __soutěžící__
- **8-bodových** méně než **10-bodových** o 1 __soutěžící__
Výpočet: 2 + 1 = 3
Závěr:**soutěž**=3 __soutěžící__ po 10 __body__
Vypočti celkem(body)?
- **soutěž**=2 __soutěžící__ po 8 __body__
- **soutěž**=5 __soutěžící__ po 9 __body__
- **soutěž**=3 __soutěžící__ po 10 __body__
- [SUM]
Závěr:**celkem**=91 __body__
Vypočti celkem(soutěžící)?
- **8-bodových**=2 __soutěžící__
- **9-bodových**=5 __soutěžící__
- **10-bodových**=3 __soutěžící__
- [SUM]
Výpočet: 2 + 5 + 3 = 10
Závěr:**celkem**=10 __soutěžící__
Rozděl 91 (body) rovnoměrně 10 krát
- **celkem**=91 __body__
- **celkem**=10 __soutěžící__
- [RATE]
Výpočet: 91 / 10 = 9,1
Závěr:**soutěž** 9,1 __body__ per __soutěžící__
**7.2 Rozbor řešení úlohy**
Co lze vyvodit na základě zadaných předpokladů?
- nejmenší počet 10-bodových platí pro počty (0,5,5) v pořadí (8-bodových, 9-bodových, 10-bodových)
- ostatní řešení získáme zvyšováním počtu 10-bodových a přesunem počtu z 9-bodových k 8-bodovým
- (0,5,5)
- (1,3,6)
- (2,1,7)
Závěr:**9-bodových**=5 __soutěžící__, **9-bodových**=3 __soutěžící__, **9-bodových**=1 __soutěžící__
---
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 8
===
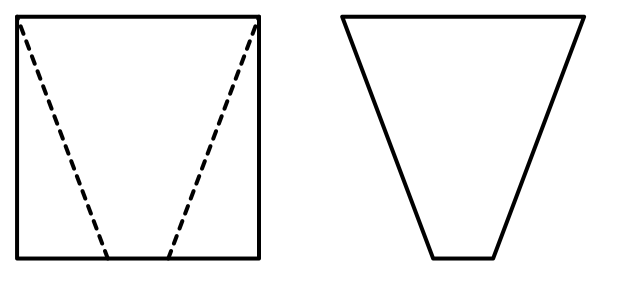
> Ze čtverce o straně délky 12 cm odstřihneme dva shodné trojúhelníky (viz obrázek vlevo).
> Vznikne tak rovnoramenný lichoběžník, jehož kratší základna má délku 2 cm.
>
> 
>
> (*CZVV*)
# 8
## 8.1 Určete, o kolik cm2 je obsah čtverce větší než obsah lichoběžníku.
## 8.2 Vypočtěte v cm obvod lichoběžníku.
[!NOTE]
**Doporučení** pro úlohy **9** a **10**: Rýsujte přímo **do záznamového archu.**
---
**8.1 Rozbor řešení úlohy**
Vypočti výraz (stranaCtverce - kratsiZakladna)/2?
- **strana čtverce**=12 __cm délka__
- **kratší základna lichoběžníku**=2 __cm délka__
- **nejkratší strana pravoúhlého trojůhelníku** = [(stranaCtverce - kratsiZakladna)/2] __cm délka__
Závěr:**nejkratší strana pravoúhlého trojůhelníku**=5 __cm délka__
Vypočti výraz 1/2 * b * h?
- **nejkratší strana pravoúhlého trojůhelníku**=5 __cm délka__
- **strana čtverce**=12 __cm délka__
- **odstřižené části - pravoúhlý trojůhelník** = [1/2 * b * h] __cm2 obsah__
Závěr:**odstřižené části - pravoúhlý trojůhelník**=30 __cm2 obsah__
Vypočti odstřižené části (2 pravoúhlé trojůhelníky)(cm2 obsah)?
- **odstřižené části - pravoúhlý trojůhelník**=30 __cm2 obsah__
- **dvojnásobek**=2
- [PRODUCT]
Výpočet: 30 * 2 = 60
Závěr:**odstřižené části (2 pravoúhlé trojůhelníky)**=60 __cm2 obsah__
**8.2 Rozbor řešení úlohy**
Vypočítej stranu nejdelší stran lichoběžník dle Pythagorovi věty?
- **nejkratší strana pravoúhlého trojůhelníku**=5 __cm délka__
- **strana čtverce**=12 __cm délka__
- [PYTHAGORAS]
Výpočet: odmocnina z (5^2 + 12^2) = 13
Závěr:**nejdelší stran lichoběžník**=13 __cm délka__
Vypočti lichoběžník(cm délka)?
- **nejdelší stran lichoběžník**=13 __cm délka__
- **nejdelší stran lichoběžník**=13 __cm délka__
- **kratší základna lichoběžníku**=2 __cm délka__
- **strana čtverce**=12 __cm délka__
- [SUM]
Výpočet: 13 + 13 + 2 + 12 = 40
Závěr:**lichoběžník**=40 __cm délka__
---
VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 11
===
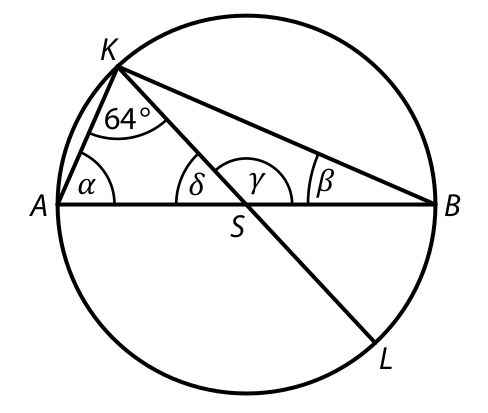
> Kružnice se středem S prochází body A, B, K, L.\
> Úsečky *AB* a *KL* se protínají v bodě S.\
> V obrázku jsou vyznačeny velikosti některých úhlů.\
>
> 
>
> (*CZVV*)
# 11 Rozhodněte o každém z následujících tvrzení (11.1–11.3), zda je pravdivé (A), či nikoli (N).
Velikosti úhlů neměřte, ale vypočtěte (obrázek je pouze ilustrativní).
## 11.1 𝛼>64°
## 11.2 𝛼+𝛽>90°
## 11.3 𝛾−𝛼>𝛿
---
**11.1 Rozbor řešení úlohy**
Kontext: *trojúhelník KAS je rovnoramenný*
Vypočti 𝛼? zadaný je schodnost úhlů při zákadně rovnoramenného trojúhelníku k 𝛼.
- **zadaný**=64 __deg úhel__
- schodnost úhlů při zákadně rovnoramenného trojúhelníku
Výpočet: 64 = 64
Závěr:**𝛼**=64 __deg úhel__
Vyhodnoť pravdivost zjištěná hodnota > 64?
- **𝛼**=64 __deg úhel__
- zjištěná hodnota > 64
Závěr:Nepravda
**11.2 Rozbor řešení úlohy**
Kontext: *thaletovo pravidlo -> trojúhelník ABK je pravoúhlý -> 𝛼 a 𝛽 = 90*
Vypočítej 𝛽 dle pravidla součtu vnitřních úhlů v trojúhelníku?
- **𝛼**=64 __deg úhel__
- **pravý úhel**=90 __deg úhel__
- [TRIANGLE-ANGLE]
Výpočet: 180 - (64 + 90) = 26
Závěr:**𝛽**=26 __deg úhel__
Vypočti 𝛼 a 𝛽(deg úhel)?
- **𝛼**=64 __deg úhel__
- **𝛽**=26 __deg úhel__
- [SUM]
Výpočet: 64 + 26 = 90
Závěr:**𝛼 a 𝛽**=90 __deg úhel__
Vyhodnoť pravdivost zjištěná hodnota > 90?
- **𝛼 a 𝛽**=90 __deg úhel__
- zjištěná hodnota > 90
Závěr:Nepravda
**11.3 Rozbor řešení úlohy**
Vypočti SKB? zadaný je doplňkový k SKB.
- **zadaný**=64 __deg úhel__
- doplňkový
Výpočet: 90 - 64 = 26
Závěr:**SKB**=26 __deg úhel__
Kontext: *trojúhelník SBK je rovnoramenný*
Vypočti 𝛽? 𝛽 je schodnost úhlů při zákadně rovnoramenného trojúhelníku k SKB.
- **SKB**=26 __deg úhel__
- schodnost úhlů při zákadně rovnoramenného trojúhelníku
Výpočet: 26 = 26
Závěr:**𝛽**=26 __deg úhel__
Vypočítej 𝛾 dle pravidla součtu vnitřních úhlů v trojúhelníku?
- **SKB**=26 __deg úhel__
- **𝛽**=26 __deg úhel__
- [TRIANGLE-ANGLE]
Výpočet: 180 - (26 + 26) = 128
Závěr:**𝛾**=128 __deg úhel__
Vypočti rozdíl mezi 𝛾 a 𝛼
- **𝛾**=128 __deg úhel__
- **𝛼**=64 __deg úhel__
- [DIFF]
Výpočet: 128 - 64 = 64
Závěr:**𝛾 - 𝛼**=64 __deg úhel__
Vypočti 𝛿? 𝛿 je vedlejší k 𝛾.
- **𝛾**=128 __deg úhel__
- vedlejší
Výpočet: 180 - 128 = 52
Závěr:**𝛿**=52 __deg úhel__
Porovnej 𝛾 - 𝛼 a 𝛿. O kolik?
- **𝛾 - 𝛼**=64 __deg úhel__
- **𝛿**=52 __deg úhel__
Výpočet: 64 - 52 = 12
Závěr:**𝛾 - 𝛼** více než **𝛿** o 12 __deg úhel__
Vyhodnoť pravdivost zjištěná hodnota > 0?
- **𝛾 - 𝛼** více než **𝛿** o 12 __deg úhel__
- zjištěná hodnota > 0
Závěr:Pravda
---
VÝCHOZÍ TEXT K ÚLOZE 12
===
> Povrch malé krychle je o 42 cm^2^ menší než povrch velké krychle.\
> Součet délek všech hran malé krychle je 36 cm.
>
> (*CZVV*)
# 12 O kolik cm^3^ se liší objem malé a velké krychle?
- [A] o 14 cm^3^
- [B] o 27 cm^3^
- [C] o 37 cm^3^
- [D] o 46 cm^3^
- [E] o jiný objem
---
**12 Rozbor řešení úlohy**
Vypočti výraz 6 * a^2?
- **malá krychle**=3 __cm délka__
- **malá krychle** = [6 * a^2] __cm2 obsah__
Závěr:**malá krychle**=54 __cm2 obsah__
Vypočti velká krychle(cm2 obsah)?
- **malá krychle**=54 __cm2 obsah__
- **velká krychle** více než **malá krychle** o 42 __cm2 obsah__
Výpočet: 54 + 42 = 96
Závěr:**velká krychle**=96 __cm2 obsah__
Vypočti výraz sqrt(S / 6)?
- **velká krychle**=96 __cm2 obsah__
- **velká krychle** = [sqrt(S / 6)] __cm délka__
Závěr:**velká krychle**=4 __cm délka__
Vypočti výraz a * a * a?
- **velká krychle**=4 __cm délka__
- **velká krychle** = [a * a * a] __cm3 objem__
Závěr:**velká krychle**=64 __cm3 objem__
Rozděl 36 (délka) rovnoměrně 12 krát
- **malá krychle**=36 __cm délka__
- **malá krychle**=12 __hran__
- [RATE]
Výpočet: 36 / 12 * 1 = 3
Závěr:**malá krychle**=3 __cm délka__
Vypočti výraz a * a * a?
- **malá krychle**=3 __cm délka__
- **malá krychle** = [a * a * a] __cm3 objem__
Závěr:**malá krychle**=27 __cm3 objem__
Porovnej velká krychle a malá krychle. O kolik?
- **velká krychle**=64 __cm3 objem__
- **malá krychle**=27 __cm3 objem__
Výpočet: 64 - 27 = 37
Závěr:**velká krychle** více než **malá krychle** o 37 __cm3 objem__
Vyhodnoť volbu [C]?
- **velká krychle** více než **malá krychle** o 37 __cm3 objem__
- Volba [C]: 37
Závěr:Volba [C]
---
VÝCHOZÍ TEXT K ÚLOZE 13
===
> Ve stanici Lichá Lhota stojí na každé ze tří kolejí jeden vlak.\
> Vlak na druhé koleji má o 3 vagony více než vlak na první koleji a dvakrát méně vagonů než vlak na třetí koleji.\
> Všechny tři vlaky dohromady mají 41 vagonů.
>
> (*CZVV*)
# 13 O kolik vagonů více má vlak na třetí koleji než vlak na první koleji?
- [A] o 8 vagonů
- [B] o 10 vagonů
- [C] o 11 vagonů
- [D] o 13 vagonů
- [E] o 14 vagonů
---
**13 Rozbor řešení úlohy**
Vyjádři výrazem s proměnnou 2.kolej(vagón)?
- **1.kolej**=x __vagón__
- **2.kolej** více než **1.kolej** o 3 __vagón__
Závěr:**2.kolej**=$ (x + 3) $ __vagón__
Vyjádři výrazem s proměnnou 3.kolej (vagón)?
- **2.kolej**=$ (x + 3) $ __vagón__
- **2.kolej** 1/2 krát méně než **3.kolej**
Závěr:**3.kolej**=$ (x + 3)\cdot \left|-\left(2\right)\right| $ __vagón__
Vyjádři výrazem s proměnnou celkem(vagón)?
- **1.kolej**=x __vagón__
- **2.kolej**=$ (x + 3) $ __vagón__
- **3.kolej**=$ (x + 3)\cdot 2 $ __vagón__
- [SUM]
Závěr:**celkem**=$ ((x + (x + 3)) + (x + 3)\cdot 2) $ __vagón__
Vyřeš lineární rovnici celkem = celkem pro neznámou x.
- **celkem**=$ ((x + (x + 3)) + (x + 3)\cdot 2) $ __vagón__
- **celkem**=41 __vagón__
- [LINEAR-EQUATION]
Závěr:**1.kolej**=8 __vagón__
Vypočti 2.kolej(vagón)?
- **1.kolej**=8 __vagón__
- **2.kolej** více než **1.kolej** o 3 __vagón__
Výpočet: 8 + 3 = 11
Závěr:**2.kolej**=11 __vagón__
Vypočti 3.kolej (vagón)?
- **2.kolej**=11 __vagón__
- **2.kolej** 1/2 krát méně než **3.kolej**
Závěr:**3.kolej**=22 __vagón__
Porovnej 3.kolej a 1.kolej. O kolik?
- **3.kolej**=22 __vagón__
- **1.kolej**=8 __vagón__
Výpočet: 22 - 8 = 14
Závěr:**3.kolej** více než **1.kolej** o 14 __vagón__
Vyhodnoť volbu [E]?
- **3.kolej** více než **1.kolej** o 14 __vagón__
- Volba [E]: 14
Závěr:Volba [E]
---
VÝCHOZÍ TEXT A GRAF K ÚLOZE 14
===
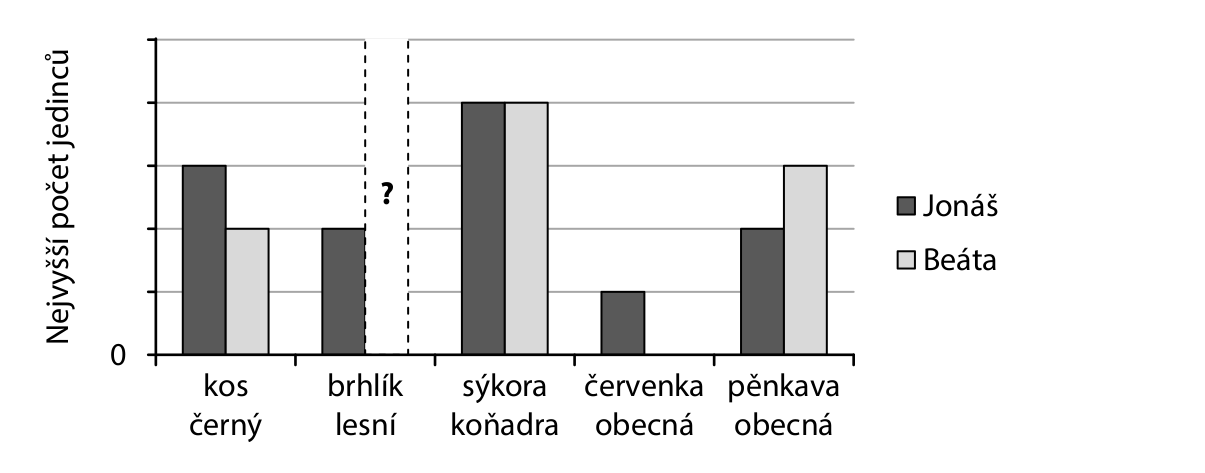
> Jonáš a Beáta se zapojili do programu Ptačí hodinka. Každý v okolí svého krmítka sledoval výskyt ptáků v průběhu jedné vybrané hodiny. U každého ptačího druhu zaznamenali do grafu vždy nejvyšší počet jedinců spatřených najednou.
>
> 
>
> Jonáš spatřil pět druhů ptáků, zatímco Beáta pouze čtyři z nich. Oba dohromady zaznamenali pěnkav o 6 méně než sýkor. Jonáš zaznamenal celkem o pětinu více ptačích jedinců než Beáta.
>
> (*CZVV*)
# 14 Kolik jedinců brhlíka lesního zaznamenala Beáta?
- [A] 2 jedince
- [B] 3 jedince
- [C] 4 jedince
- [D] 5 jedinců
- [E] více než 5 jedinců
---
**14 Rozbor řešení úlohy**
Porovnej pěnkavy a sýkory. O kolik?
- **pěnkavy**=5 __dílek__
- **sýkory**=8 __dílek__
Výpočet: 5 - 8 = -3
Závěr:**pěnkavy** méně než **sýkory** o 3 __dílek__
Rozděl (ptáci) rovnoměrně na (dílek)
- **pěnkavy** méně než **sýkory** o 3 __dílek__
- **pěnkavy** méně než **sýkory** o 6 __ptáci__
- [RATE]
Výpočet: 6 / 3 = 2
Závěr:**jednotka grafu** 2 __ptáci__ per __dílek__
Vypočti Jonáš(ptáci)?
- **jednotka grafu** 2 __ptáci__ per __dílek__
- **Jonáš**=12 __dílek__
Výpočet: 12 * 2 = 24
Závěr:**Jonáš**=24 __ptáci__
Vypočti Beata (ptáci)?
- **Jonáš**=24 __ptáci__
- **Jonáš** více o 1/5 než **Beata**
Výpočet: 24 / 6/5 = 20
Závěr:**Beata**=20 __ptáci__
Vypočti Beata(ptáci)?
- **Beata**=9 __dílek__
- **jednotka grafu** 2 __ptáci__ per __dílek__
Výpočet: 9 * 2 = 18
Závěr:**Beata**=18 __ptáci__
Vypočti rozdíl mezi Beata a Beata
- **Beata**=20 __ptáci__
- **Beata**=18 __ptáci__
- [DIFF]
Výpočet: 20 - 18 = 2
Závěr:**brhlík lesní**=2 __ptáci__
Vyhodnoť volbu [A]?
- **brhlík lesní**=2 __ptáci__
- Volba [A]: 2
Závěr:Volba [A]
---
# 15 Přiřaďte ke každé úloze (15.1–15.3) odpovídající výsledek (A–F).
## 15.1
Pan Zdeněk bydlí posledních pět osmin svého dosavadního života v Plzni,
kam se přestěhoval, když mu bylo 27 let.
**Kolik let bydlí pan Zdeněk v Plzni?**
## 15.2
Ze tří škol v obci je nejstarší základní škola, která je v provozu již 84 let.
Funguje tedy o 75 % delší dobu než gymnázium. Nejmladší školou je lyceum.
Poměr doby fungování lycea a gymnázia je 2∶3.
**Kolik let funguje v obci lyceum?**
## 15.3
Součet věků dvojčat a jejich staršího bratra je 99 let.
Každému z dvojčat je o 40 % méně let než jejich bratrovi.
**Kolik let je každému z dvojčat?**
- [A] 22 let
- [B] 27 let
- [C] 32 let
- [D] 45 let
- [E] 48 let
- [F] více než 48 let
---
**15.1 Rozbor řešení úlohy**
Vyjádři poměrem život před přestěhováním do Plzně z celý život?
- **život v Plzni** z **celý život**=5/8
- [COMPLEMENT]
Výpočet: 1 - 5/8 = 3/8
Závěr:**život před přestěhováním do Plzně** z **celý život**=3/8
Vypočti celý život(let)?
- **život před přestěhováním do Plzně** z **celý život**=3/8
- **život před přestěhováním do Plzně**=27 __let__
Výpočet: 27 / 3/8 = 72
Závěr:**celý život**=72 __let__
Vypočti rozdíl mezi celý život a život před přestěhováním do Plzně
- **celý život**=72 __let__
- **život před přestěhováním do Plzně**=27 __let__
- [DIFF]
Výpočet: 72 - 27 = 45
Závěr:**život v Plzni**=45 __let__
Vyhodnoť volbu [D]?
- **život v Plzni**=45 __let__
- Volba [D]: 45
Závěr:Volba [D]
**15.2 Rozbor řešení úlohy**
Vypočti gymnázium (let)?
- **základní škola**=84 __let__
- **základní škola** více o 75% než **gymnázium**
Výpočet: 84 / 7/4 = 48
Závěr:**gymnázium**=48 __let__
Vypočti lyceum(let)?
- **gymnázium**=48 __let__
- **poměr doby fungování** **lyceum**:**gymnázium** v poměru 2:3
- **lyceum**
Výpočet: 48 / 3 * 2 = 32
Závěr:**lyceum**=32 __let__
Vyhodnoť volbu [C]?
- **lyceum**=32 __let__
- Volba [C]: 32
Závěr:Volba [C]
**15.3 Rozbor řešení úlohy**
Vyjádři poměrem částí dvojče:dvojče:starší bratr?
- **dvojče** méně o 40% než **starší bratr**
- **dvojče** méně o 40% než **starší bratr**
- [RATIOS]
Výpočet: (3/5,3/5) v poměru k 1 = 3/5:3/5:1
Závěr:**věk bratrů** **dvojče**:**dvojče**:**starší bratr** v poměru 0,6:0,6:1
Vypočti starší bratr(let)?
- **věk bratrů** **dvojče**:**dvojče**:**starší bratr** v poměru 0,6:0,6:1
- **věk bratrů**=99 __let__
Výpočet: 99 / (0.6 + 0.6 + 1) * 1 = 45
Závěr:**starší bratr**=45 __let__
Vypočti dvojče (let)?
- **starší bratr**=45 __let__
- **dvojče** méně o 40% než **starší bratr**
Výpočet: 45 * 3/5 = 27
Závěr:**dvojče**=27 __let__
Vyhodnoť volbu [B]?
- **dvojče**=27 __let__
- Volba [B]: 27
Závěr:Volba [B]
---